Vectors (R)
Basics of vectors¶
Consider two vectors a and b
a <- c(1,2)
b <- c(1,1)
The two vectors can be visualised in a 2D coordinate system as follows:
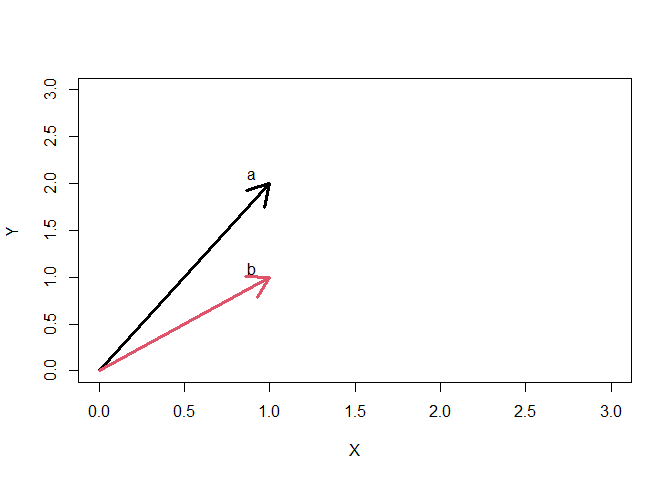
We can perform two types of linear operations on these vectors:
1. Vector addition
2. Multiplication of the vector with a scalar
Vector addition:
If we add a and b together, the sum would be a vector whose members are the sum of the corresponding members from a and b.
a+b
## [1] 2 3
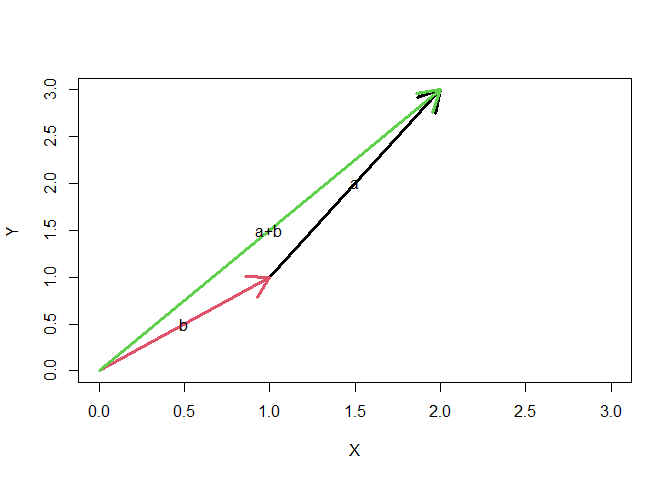
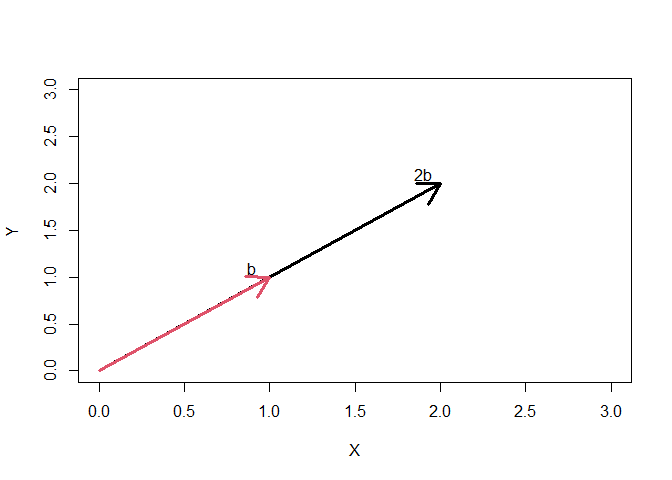
Vector multiplication: If we multiply b by 2, we will get a vector with each of its members multiplied by 2.
2*b
## [1] 2 2
Subspaces and span¶
As we can perform only two kinds of linear operations on the vectors, any linear combinations will be of the form:
$$ S= \alpha a + \beta b $$ Where \(\alpha\) and \(\beta\) are real numbers and \(a\) and \(b\) are vectors.
What about all possible linear combinations of \(a\) and \(b\)?

The linear combination of the vector a and b form the entire 2D plane.
Vector space is the space in which the vector can exist. A 2D vector, like a or b, will have vector space of \(R^2\) and a 3D vector like d=[1,2,3] is in the vector space \(R^3\).
Span: The set of all possible linear combinations of vectors is called the span of those set of vectors.
For the above two vectors a = [1,2] and b=[1,1], the entire 2d space is the span, as we can get every vector in the 2d space as a linear combination of the two vectors.
To explain the difference between vector space and vector span, consider the two vectors d=[1,2,3] and e=[1,1,1] As the two vectors are in 3 dimensions, they have a vector space of 3 or \(R^3\).
Adding d+e I get another vector in 3d.
d <- c(1,2,3)
e <- c(1,1,1)
d+e
## [1] 2 3 4
But what are all the linear combinations for d and e?

This forms a 2d plane which goes thru the origin. Therefore these vectors span a plane (in \(R^2\)) although their vector space is (\(R^3\)).
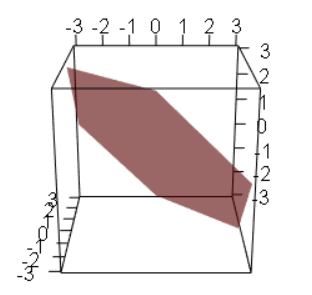
The maximum span that any set of vectors can have is equal to their vector space.
Linear Independence¶
Linear independence is when one vector has no relationship with another. In the first example with a=[1,2] and b=[1,1], any vectors in the 2d space can be written as a linear combination of a and b. In the second example with d=[1,2,3] and e=[1,1,1], any vector on the plane can be written as a linear combination of d and e. A vector which is not in the plane, like f = [2,3,3] is linearly independent of d and e, as no \(\alpha\) and \(\beta\) satisfy \(f=\alpha d+\beta e\).
In a vector space of n dimensions (vector space is n), there can be at max n vectors which are linearly independent.
Bases, norms and inner products¶
A basis for \(R^n\) space is any linearly independent set of vectors S such that span(S) = n.
From the above examples, a and b are in the vector space \(R^2\) and also have their span as \(R^2\). Therefore they form a basis for \(R^2\).
Similarly, the three independent vectors d, e and f are in the vector space \(R^3\) and form a basis for \(R^3\).
The standard basis for \(R^2\) is [1.0] and [0,1].
The norm of the vector is the length of the vector.
norm(a, type="2")
## [1] 2.236068
norm(d, type="2")
## [1] 3.741657
The dot product (or inner product) takes two vectors as an input and returns a number as an output. It is defined as \(\bar{x}.\bar{y} = \sum{x_i\times y_i}\). It represents the length of the shadow of one vector on the other.
library(geometry)
dot(a,b)
## [1] 3
In the next post in this series, I will talk about matrices.