Shortest path problems¶

Author: Achyuthuni Sri Harsha
Shortest path is one problem in networks which appears in many forms across many industries. It tells the user how to find the shortest path between two pairs of nodes. In this particular example, we will look at finding the shortest path between a pair of nodes in a directed network using an integer programming solver.

import networkx as nx

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Consider the following simple weighted directed network, with four nodes and five edges.

edgelist_df = pd.DataFrame({'node1':['s', 's', 'u', 'u', 'v'], 'node2':['u', 'v', 'v', 't', 't'], 
                            'weights':[3, 2, 0.7, 1, 7]
                           })
edgelist_df

	node1	node2	weights
0	s	u	3.0
1	s	v	2.0
2	u	v	0.7
3	u	t	1.0
4	v	t	7.0

g = nx.DiGraph()
for i, elrow in edgelist_df.iterrows():
    g.add_edge(elrow[0], elrow[1], weight=elrow[2])
g.edges(data=True)

OutEdgeDataView([('s', 'u', {'weight': 3.0}), ('s', 'v', {'weight': 2.0}), ('u', 'v', {'weight': 0.7}), ('u', 't', {'weight': 1.0}), ('v', 't', {'weight': 7.0})])

# for each node we are trying to fix the coordinates
g.add_node('s',pos=(0,1))
g.add_node('u',pos=(1,2))
g.add_node('v',pos=(1,0))
g.add_node('t',pos=(2,1))
g.nodes(data=True)

NodeDataView({'s': {'pos': (0, 1)}, 'u': {'pos': (1, 2)}, 'v': {'pos': (1, 0)}, 't': {'pos': (2, 1)}})

# This function gets the coordinates for nodes
pos = nx.get_node_attributes(g,'pos')

# This function gets the weights for the edges 
weight = nx.get_edge_attributes(g,'weight')


nx.draw(g,pos, with_labels=True)
nx.draw_networkx_edge_labels(g,pos,edge_labels = weight)
plt.show()

png

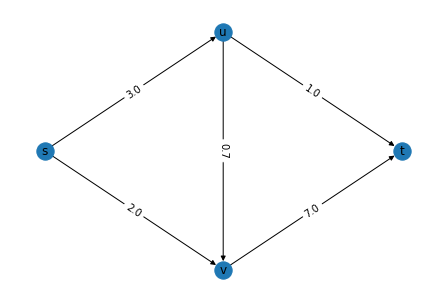
Now, we want to find the shortest path between the node 's' and 't'. In this network, edge-weights represent the costs for each edge. The weights could be distance, or time. NetworkX has an inbuilt function shortest_path which returns the shortest path. Using NetworkX, we get the following shortest path:

path_2_0 = nx.shortest_path(g, source ='s',target = 't')
path_2_0

['s', 'u', 't']

Formulating the problem using integer programming¶

We have n nodes V and m edges E (n=4, m=5 for this example). OR tools is an open source software built by Google for solving integer programming problems. Cp-Sat solver is one such model by OR Tools, which we are going to use today.

We can use binary decision variables \(edge_{i,j}\) representing the edge that goes from node i to node j. If \(edge_{i,j}=1\) the shortest path belongs to the path between i and j, 0 otherwise.

from ortools.sat.python import cp_model
shortest_path_model = cp_model.CpModel()

# Creating one integer decision variable for each edge
edge_bool_vars = {}
for edge in g.edges:
    edge_bool_vars[edge[0], edge[1]] = shortest_path_model.NewBoolVar('edge_%s_%s' % edge)
    print('Creating the boolean variable ', edge_bool_vars[edge[0], edge[1]], 
          'representing the if we should travel through ', (edge[0], edge[1]))

Creating the boolean variable  edge_s_u representing the if we should travel through  ('s', 'u')
Creating the boolean variable  edge_s_v representing the if we should travel through  ('s', 'v')
Creating the boolean variable  edge_u_v representing the if we should travel through  ('u', 'v')
Creating the boolean variable  edge_u_t representing the if we should travel through  ('u', 't')
Creating the boolean variable  edge_v_t representing the if we should travel through  ('v', 't')

The shortest path (in isolation) will have the following properties:
1. Starting node has a degree -1
2. Ending node has a degree +1
3. All intermediary nodes have degree 0

This can be written in the form of flow balance constraints as follows:

input_node = 's'
output_node = 't'

# Adding constraints on the nodes
for node in g.nodes:
    in_edges = g.in_edges(node)
    out_edges = g.out_edges(node)
    print('Adding the constraint on node ', node)
    print('This node has %i in-edges and %i out-edges' % (len(in_edges), len(out_edges)))
    equation_at_this_edge = sum(edge_bool_vars[edge[0], edge[1]] for edge in in_edges) - \
                            sum(edge_bool_vars[edge[0], edge[1]] for edge in out_edges)
    if(node == input_node):              
        shortest_path_model.Add(equation_at_this_edge == -1)
        print(equation_at_this_edge == -1)
    elif(node == output_node):              
        shortest_path_model.Add(equation_at_this_edge == 1)
        print(equation_at_this_edge == 1)
    else:
        shortest_path_model.Add(equation_at_this_edge == 0)
        print(equation_at_this_edge, '== 0')
    print('')

Adding the constraint on node  s
This node has 0 in-edges and 2 out-edges
(-((edge_s_u) + edge_s_v)) == -1

Adding the constraint on node  u
This node has 1 in-edges and 2 out-edges
((edge_s_u) + -((edge_u_v) + edge_u_t)) == 0

Adding the constraint on node  v
This node has 2 in-edges and 1 out-edges
(((edge_s_v) + edge_u_v) + -(edge_v_t)) == 0

Adding the constraint on node  t
This node has 2 in-edges and 0 out-edges
(((edge_u_t) + edge_v_t)) == 1

The objective of the shortest path problem is to find the path with the minimum cost. This can be written as minimising the costs as follows:

# factor to make everything including costs integer
factor_to_int = 10

# The objective is to maximise flow 
total_cost = sum(int(g.get_edge_data(*edge)['weight']*factor_to_int)*edge_bool_vars[edge[0], edge[1]]
                for edge in g.edges)

print('Objective is to optimise cost')
print(total_cost)
shortest_path_model.Minimize(total_cost)

Objective is to optimise cost
((((((30 * edge_s_u)) + (20 * edge_s_v)) + (7 * edge_u_v)) + (10 * edge_u_t)) + (70 * edge_v_t))

Solving the problem, we have an optimal solution with the overall cost as 40 units.

# Solving the problem
solver = cp_model.CpSolver()
solution_printer = cp_model.ObjectiveSolutionPrinter()
status = solver.SolveWithSolutionCallback(shortest_path_model, solution_printer)

Solution 0, time = 0.02 s, objective = 40

cp_model.OPTIMAL == status

True

The solution is given as

result_edges = {}
for edge in g.edges:
    result_edges[edge[0], edge[1]] = solver.Value(edge_bool_vars[edge[0], edge[1]])
result_edges

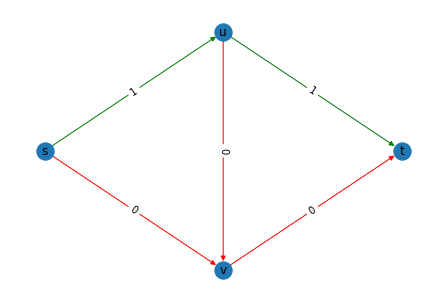
{('s', 'u'): 1, ('s', 'v'): 0, ('u', 'v'): 0, ('u', 't'): 1, ('v', 't'): 0}

Plotting the network in such a way that the green lines represent the shortest path, we get

pos = nx.get_node_attributes(g,'pos')
color = ['g' if val==1 else 'r' for val in result_edges.values()]

nx.draw(g,pos, with_labels=True, edge_color= color)

nx.draw_networkx_edge_labels(g,pos,edge_labels = result_edges)
plt.show()

png

References¶

Modelling and optimisation over networks, Network Analytics module, Kalyan Talluri, MSc Business analytics, Imperial College London, Class 2020-22